Méthode 3 - Trouver le sens de variation et l'extrémum d'un polynôme du seconde degré

Soit la fonction $Mathplace quicklatex.com-b0cbdaef4463694ab7a15df0747956c7_l3 Méthode 3 - Trouver le sens de variation et l'extrémum d'un polynôme du seconde degré$ .

Il s’agit d’un polynôme du second degré de la forme de $Mathplace quicklatex.com-f856438660a2b836b86b1bb9a4ac9758_l3 Méthode 3 - Trouver le sens de variation et l'extrémum d'un polynôme du seconde degré$ avec $Mathplace quicklatex.com-b548292d86ab9fb2c396f88f16b8c998_l3 Méthode 3 - Trouver le sens de variation et l'extrémum d'un polynôme du seconde degré$ , $Mathplace quicklatex.com-0b9c31dd6ee8ee94890660e2c7909ed9_l3 Méthode 3 - Trouver le sens de variation et l'extrémum d'un polynôme du seconde degré$ et $Mathplace quicklatex.com-7941cdee36f92c02d4d5c4d6200575bb_l3 Méthode 3 - Trouver le sens de variation et l'extrémum d'un polynôme du seconde degré$ .

Sa courbe représentative est donc une parabole avec pour sommet le point $Mathplace quicklatex.com-1a1de0aa0f6c68b470df94a4ba6b2bba_l3 Méthode 3 - Trouver le sens de variation et l'extrémum d'un polynôme du seconde degré$ de coordonnées $Mathplace quicklatex.com-963effd4510f9d84e10327576e2797c8_l3 Méthode 3 - Trouver le sens de variation et l'extrémum d'un polynôme du seconde degré$ .

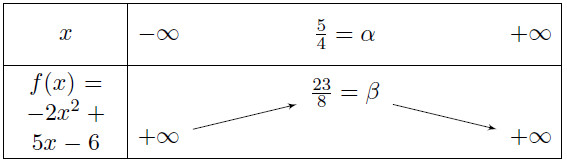
Pour construire notre tableau de variation nous avons besoin de calculer l’extrémum $Mathplace quicklatex.com-6623b868aa0b6a758e58ec9c217b6bec_l3 Méthode 3 - Trouver le sens de variation et l'extrémum d'un polynôme du seconde degré$ de la courbe ainsi que la valeur de x pour lequel on l’obtient $Mathplace quicklatex.com-51b8c2611c298b92b8c616babf6d79f3_l3 Méthode 3 - Trouver le sens de variation et l'extrémum d'un polynôme du seconde degré$ .

Ainsi,

$Mathplace quicklatex.com-e6fc3d5bc854d1f7a2c8d5104530ee69_l3 Méthode 3 - Trouver le sens de variation et l'extrémum d'un polynôme du seconde degré$

$Mathplace quicklatex.com-846fed2dfc4d0d656442541dc6196eb3_l3 Méthode 3 - Trouver le sens de variation et l'extrémum d'un polynôme du seconde degré$

L’extremum est donc $Mathplace quicklatex.com-d77d37c71508f9240e11ac5bcf9990eb_l3 Méthode 3 - Trouver le sens de variation et l'extrémum d'un polynôme du seconde degré$ pour $Mathplace quicklatex.com-e97e8ea92d823cbf1e1a4c70fe809a4d_l3 Méthode 3 - Trouver le sens de variation et l'extrémum d'un polynôme du seconde degré$ .

Remarque :

Si la forme canonique de la fonction vous est donnée vous avez déjà les coordonnées $Mathplace quicklatex.com-42421223af7c58fb1e03b6ed869a4ef7_l3 Méthode 3 - Trouver le sens de variation et l'extrémum d'un polynôme du seconde degré$ et $Mathplace quicklatex.com-6623b868aa0b6a758e58ec9c217b6bec_l3 Méthode 3 - Trouver le sens de variation et l'extrémum d'un polynôme du seconde degré$ dans l’expression.

On analyse ensuite le signe de $Mathplace quicklatex.com-139813192e94b132893033c54bbdb71c_l3 Méthode 3 - Trouver le sens de variation et l'extrémum d'un polynôme du seconde degré$ .

Ici $Mathplace quicklatex.com-139813192e94b132893033c54bbdb71c_l3 Méthode 3 - Trouver le sens de variation et l'extrémum d'un polynôme du seconde degré$ est négatif, la parabole est donc orientée vers le bas, la fonction est strictement croissante sur $Mathplace quicklatex.com-a5c8fa75431809be40b3f7b7711e0852_l3 Méthode 3 - Trouver le sens de variation et l'extrémum d'un polynôme du seconde degré$ et strictement décroissante sur $Mathplace quicklatex.com-e55b2f09ad643d15542e8d453d9c7f0a_l3 Méthode 3 - Trouver le sens de variation et l'extrémum d'un polynôme du seconde degré$ .