Pour calculer le produit scalaire de deux vecteurs ![]() ,
, ![]() , on peut déterminer le projeté orthogonal
, on peut déterminer le projeté orthogonal ![]() de
de ![]() sur
sur ![]() et utiliser le résultat suivant :
et utiliser le résultat suivant :
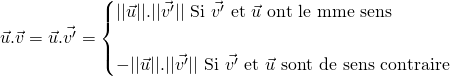
Etape 1 : faire la projection du vecteur ![]() sur
sur ![]() (voir figure)
(voir figure)

Etape 2 : Déterminer la norme ![]() et appliquer la formule présenter plus haut.
et appliquer la formule présenter plus haut.
Exemple 1 :
Considérons le schéma suivant :

Déterminer dans chaque cas le produit scalaire ![]() .
.
Cas 1-A : ![]() (
(![]() )
)
Cas 1-B : ![]() (
(![]() )
)
Cas 2-A : ![]() (
(![]() )
)
Cas 2-B : ![]() (
(![]() )
)
Exemple 2 :
Un cas plus pratique
Considérons le rectangle ![]() avec
avec ![]() et
et ![]() .
.
Déterminer les produits scalaires suivant :
![]() ;
; ![]()
On a la représentation suivante :

Le projeté orthogonal de ![]() sur
sur ![]() est égale à
est égale à ![]() , donc
, donc
![]() =
= ![]() =
= ![]() =
= ![]() .
.
Le projeté orthogonal de ![]() sur
sur ![]() est égale à \vec{BA}
est égale à \vec{BA}![]() \vec{AB}.\vec{BD}
\vec{AB}.\vec{BD}![]() \vec{AB}.\vec{BA}
\vec{AB}.\vec{BA}![]() \vec{AB}.\vec{AB}
\vec{AB}.\vec{AB}![]() -\Vert \vec{AB} \Vert^2
-\Vert \vec{AB} \Vert^2![]() -3^2=-9$.
-3^2=-9$.