Voici deux méthodes pour montrer que deux plans sont parallèles :
- On montre que ces deux plans sont parallèles à un même plan et donc parallèles entre eux.
- L’autre méthode consiste à considérer deux droites sécantes du même plan, puis de montrer que ces deux droites sont parallèles à l’autre plan.
La méthode à choisir sera fonction de l’exercice et de ses donnés.
Exemple 1 :
Soit 
le parallélépipède et 
le milieu du segment 
. On considère le plan 
parallèle à 
et passant par .
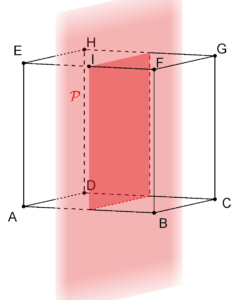
Démontrons que le plan est parallèle à 
.
Pour se faire nous utiliserons ici la première méthode.
- Nous savons que les faces opposées d’un parallélépipède sont parallèles deux à deux, ainsi les plans 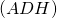et 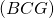sont parallèles. L’énoncé nous renseigne que le plan 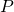est également parallèle à .
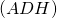- Or d’après la propriété du cours deux plans parallèles à un même plan sont parallèles entre eux.
- On en déduit que 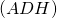et 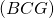sont parallèles.
&nb
