A – Positions relatives entre deux droites
Propriétés :
Deux droites peuvent être entre elles :
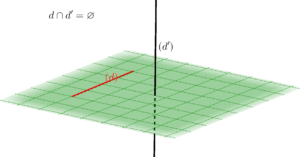
- non coplanaires : leur intersection est alors un ensemble vide.
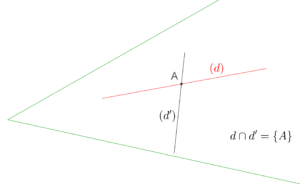
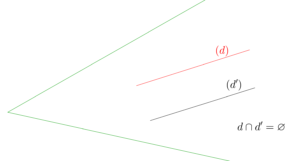
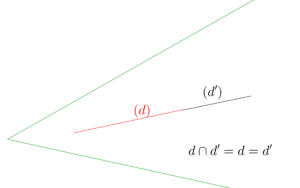
- coplanaires : plusieurs cas possibles, les deux droites peuvent être sécantes, parallèles ou confondues. L’intersection des deux droites est alors selon les cas, respectivement un point, l’ensemble vide ou une droite.
| Droites coplanaires |
| Droites sécantes |
 |
| Droites parallèles |
 |
| Droites confondues |
 |
| Droites non coplanaires |
 |
Remarque :
Contrairement au plan, deux droites non sécantes dans l’espace ne sont pas forcément parallèles.
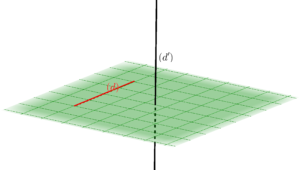
B/ Positions relatives entre une droite et un plan
Propriété :
Une droite ![]() et un plan
et un plan ![]() de l’espace peuvent être :
de l’espace peuvent être :
- sécants : l’intersection entre la droite et le plan est alors un point.
- parallèles : deux cas possibles, soit
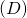 est contenue dans le plan
est contenue dans le plan 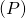 et leur intersection est la droite
et leur intersection est la droite 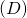 , soit
, soit 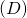 n’est pas contenue dans le plan
n’est pas contenue dans le plan 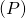 et leur intersection est l’ensemble vide.
et leur intersection est l’ensemble vide.
| Droite et plan sécants | |
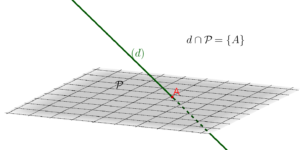 |
|
| Droite et plan parallèles | |
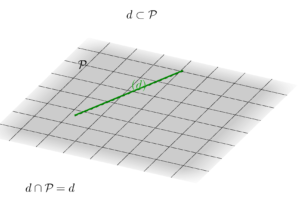 |
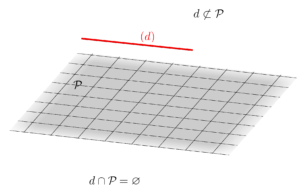 |
C – Positions relatives entre deux plans
Propriété :
Deux plans de l’espace ![]() et
et ![]() peuvent être :
peuvent être :
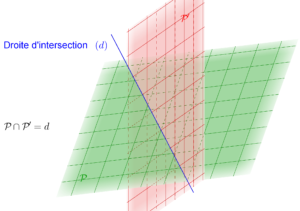
- sécants : l’intersection entre
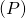 et
et 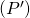 est une droite.
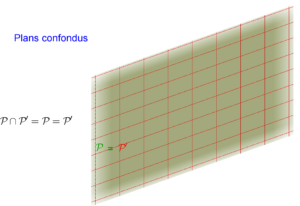
est une droite. - parallèles : deux cas possibles, soit
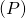 et
et 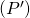 sont confondus et leur intersection est le plan
sont confondus et leur intersection est le plan 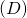 , soit
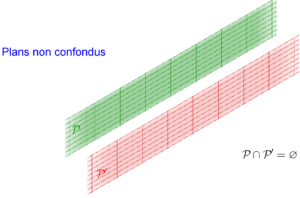
, soit 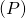 et
et 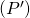 ne sont pas confondus et leur intersection est l’ensemble vide.
ne sont pas confondus et leur intersection est l’ensemble vide.
| Plans sécants | |
 |
|
| Plans parallèles | |
 |
 |
Remarque :
Si deux plans ![]() et
et ![]() ne sont pas sécants alors ils sont parallèles entre eux.
ne sont pas sécants alors ils sont parallèles entre eux.