Principe :
Pour montrer qu’une droite est parallèle à un plan on peut montrer que cette droite est parallèle à une autre droite incluse dans le plan en question.
Application :
Soit le tétraèdre ![]() suivant, avec
suivant, avec ![]() et
et ![]() les milieux respectifs de
les milieux respectifs de ![]() et
et ![]() .
.
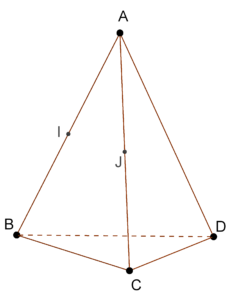
On souhaite montrer que ![]() et
et ![]() sont parallèles.
sont parallèles.
- En se plaçant dans le triangle
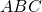 et en utilisant le théorème des milieux (avec I et J les milieux) on en déduit que les droites
et en utilisant le théorème des milieux (avec I et J les milieux) on en déduit que les droites 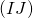 et (BC) sont parallèles.
et (BC) sont parallèles. - Or
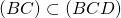 .
.
On en déduit donc que ![]() est parallèle à
est parallèle à ![]() .
.
nt parallèles.
On en déduit donc que ![]() est parallèle à
est parallèle à