Pour étudier le sens de variation d’une fonction définie par ![]() :
:
Etape 1 : Mettre ![]() sous la forme canonique :
sous la forme canonique :
![]() où
où ![]() et
et ![]()
Etape 2 :
- Si
 alors la fonction f est croissante sur l’intervalle
alors la fonction f est croissante sur l’intervalle 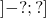 et décroissante sur
et décroissante sur 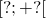 .
. - Si
 alors la fonction
alors la fonction 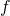 est décroissante sur l’intervalle
est décroissante sur l’intervalle 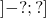 et croissante sur
et croissante sur 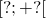
On a les tableaux suivants :
| Si a>0 | Si a<0 |
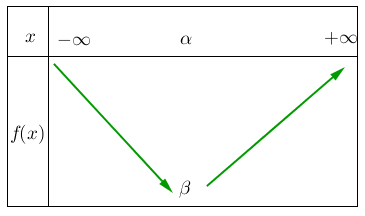 |
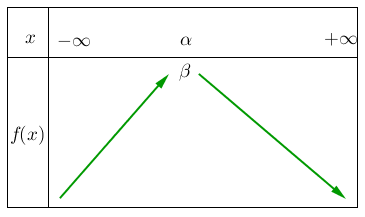 |
Exemple
Etudions les variations des fonctions suivantes : ![]() et
et ![]()
Pour la fonction ![]() , il est immédiat que sur l’intervalle
, il est immédiat que sur l’intervalle ![]() ,
, ![]() est croissante et sur l’intervalle
est croissante et sur l’intervalle ![]() est décroissante.
est décroissante.
Le sommet de ![]() est le point de coordonnées
est le point de coordonnées ![]() .
.
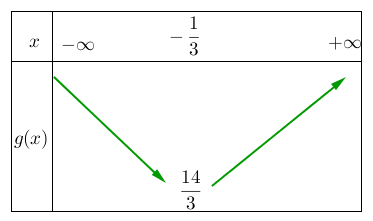
On a le tableau suivant :
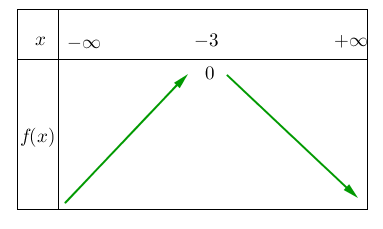
Pour la fonction ![]() on a :
on a :
![]()
Donc il suit que sur l’intervalle ![]() ,
, ![]() est décroissante et sur l’intervalle
est décroissante et sur l’intervalle ![]() est croissante.
est croissante.
Le sommet de ![]() est le point de coordonnées
est le point de coordonnées ![]() .
.
On a le tableau suivant :