1) Soit 
la fonction définie sur 
par 
.
a- Etudier les variations de .
b- Deduire le signe de .
2) Soit 
la fonction définie sur par 
et 
sa courbe reprèsentative.
a- Calculer la derivée 
de et exprimer 
en fonction de 
.
b- Déduire le sens de variaton de .
c- Preciser les limites aux bornes de l’ensemble de définition de .
d- Démontrer que la droite 
d’équation 
est asymptote a .
1) .
a- Etudions les variations de , 
est dérivable sur 
et sa derivee est 
D’où 
a pour solution 
où 
or 
, d’où 
.
Tableau de variation
b- D’après le tableau de variation, croit de 
a 
, puis decroit de 
a , d’où est negative 
.
2)
a-
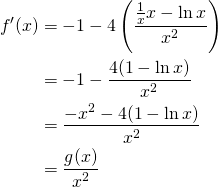
b- 
sur car 
et donc est strictement décroissante sur .
c- se prèsente comme une somme donc on calcule la limite de chaque terme
$\lim_{x\rightarrow 0
