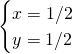Etant donnés deux vecteurs 
et 
formant une base du plan, pour déterminer les coordonnées d’un vecteur 
dans la base 
:
Etape 1 : On pose 
Etape 2 : On remplace 
et 
par leurs coordonnées, on obtient :
Etape 3 : Comme alors par identification, on a :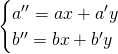 
Etape 4 : on résout le système précédant et on trouve 
et 
.
Etape 5 : les coordonnées de 
dans sont 
Exemple
Considérons les vecteurs 
, 
et 
Montrer que forment une base du plan
Déterminer les coordonnées de dans
On a 
d’où forment une base du plan
Posons et déterminons et .
On a 
Comme a , il vient par identification que :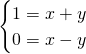 
d’où 
