Exercice de synthese
Dans un repère orthonormé 
, on donne les points 
, 
et 
.
Soit 
le projeté orthogonal de 
sur 
.
1/ Calculer les coordonnées de .
2/ En déduire la distance de à la droite , c’est-à-dire la plus courte distance de à un point quelconque de .
3/ Calculer l’aire du triangle 
.
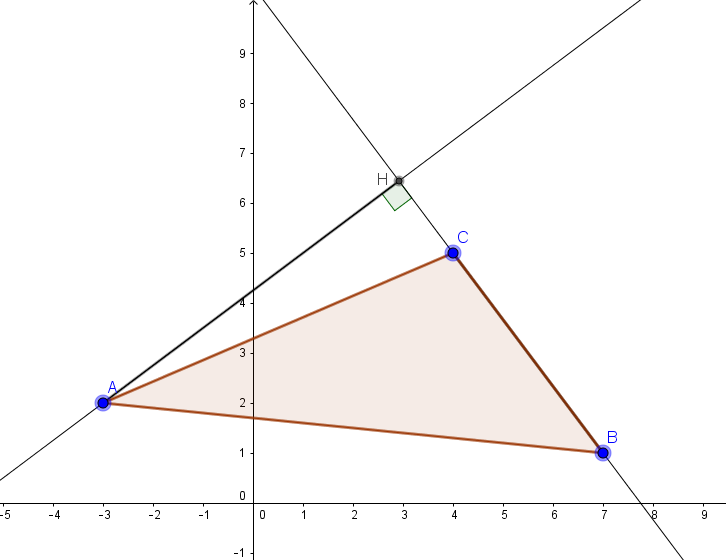
1/ Déterminons les coordonnées de
Déterminons une équation de
Une équation de est 
Soit 
, un vecteur directeur de la droite est : 
Le vecteur 
.
Les coordonnées de sont les solutions du système
On résout le système :
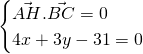
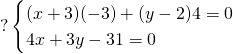
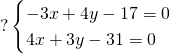
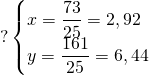
2/ La distance de à la droite , c’est la distance 
qui est égale à :
3/ Calculons l’aire du triangle .
En considérant que la base du triangle est 
, la hauteur du triangle est .
Ainsi 
or 
et en calculant on obtient 
D’où :
[/bg_collapse]
ire du triangle .
En considérant que la base du triangle est , la hauteur du triangle est .
Ainsi or et en calculant on obtient
D’où :
$A_{\text{aire de ABC
