Exercice 5 : Application de la dérivée

Soit une fonction rationnelle dont le tableau de variation ci-dessous est celui de la dérivée .

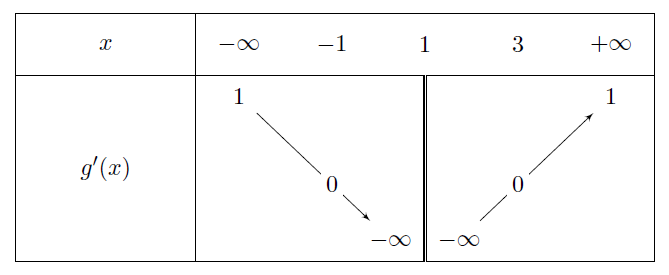
1/ Déduire du tableau de variation de

a) L’ensemble de définition de

b) Le signe de suivant les valeurs de

c) Les variations de

d) Les abscisses des points où la tangente parallèle à l’axe des abscisses

2/ On suppose que la droite d’équation : est un axe de symétrie de la fonction .

Demontrer que pour tout , les tangentes à la courbe de aux abscisses et sont parallèles.

Voir/Cacher la solution
 

1/

a) Une fonction rationnelle a le même ensemble de définition que sa dérivée :

b) Signe de (Dans un tableau de signe) :

c) est croissante sur $]-\infty,