Pour représenter une expérience aléatoire on peut utiliser un arbre pondéré qui facilitera la visualisation des différentes issues possibles. Celui-ci est surtout pratique lorsque l’expérience aléatoire est constituée de plusieurs évènements indépendants.
L’arbre pondéré doit respecter les règles suivantes :
- Chaque évènement est représenté par une ramification donnant naissance à un nombre de branches égale au nombre d’issues possibles de l’évènement considéré.
- Le nombre de branches en fin d’arbre correspond à tous les résultats possibles de l’expérience.
- On écrit sur chaque branche la probabilité de l’issue considérée.
- On peut calculer la probabilité d’un résultat obtenu lors de l’expérience, en multipliant les probabilités rencontrées sur l’arbre lorsqu’on retrace le chemin aboutissant au résultat considéré.
Prenons l’exemple de l’expérience aléatoire où l’on tire au hasard successivement deux boules parmi six boules dont quatre sont blanches et deux sont noires.
Le premier évènement correspond à la couleur de la première boule tirée parmi six (sans remise dans l’urne). Le deuxième évènement correspond à la couleur de la deuxième boule tirée parmi cinq boules.
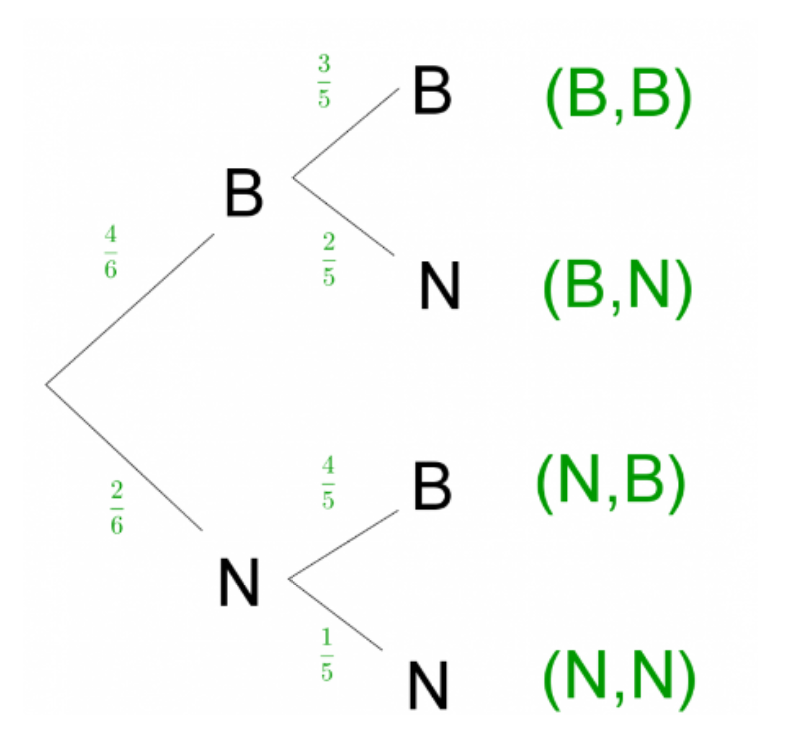
Voilà l’arbre correspondant avec 
pour l’évènement « tirer une boule blanche », 
« tirer une boule noire ». Les probabilités de chaque évènement sont écrits sur les branches.
Pour le premier tirage on a une probabilité de 
d’obtenir une boule blanche et une probabilité de 
d’obtenir une boule noire.
Lors du deuxième tirage sachant que l’on a déjà retiré une boule, il reste plus que cinq boules dans l’urne.
Si la première boule tirée est noire, il ne reste plus qu’une boule noire et toujours quatre boules blanches dans l’urne. Ainsi, au deuxième tirage, la probabilité de tirer une boule noire sera de 
et celle de tirer une boule blanche sera de 
.
Si la première boule est blanche, alors il ne reste dans l’urne que trois boules blanches et deux boules noires. Les probabilités au deuxième tirage d’obtenir une boule blanche ou une boule noire sont respectivement de 
ou 
.
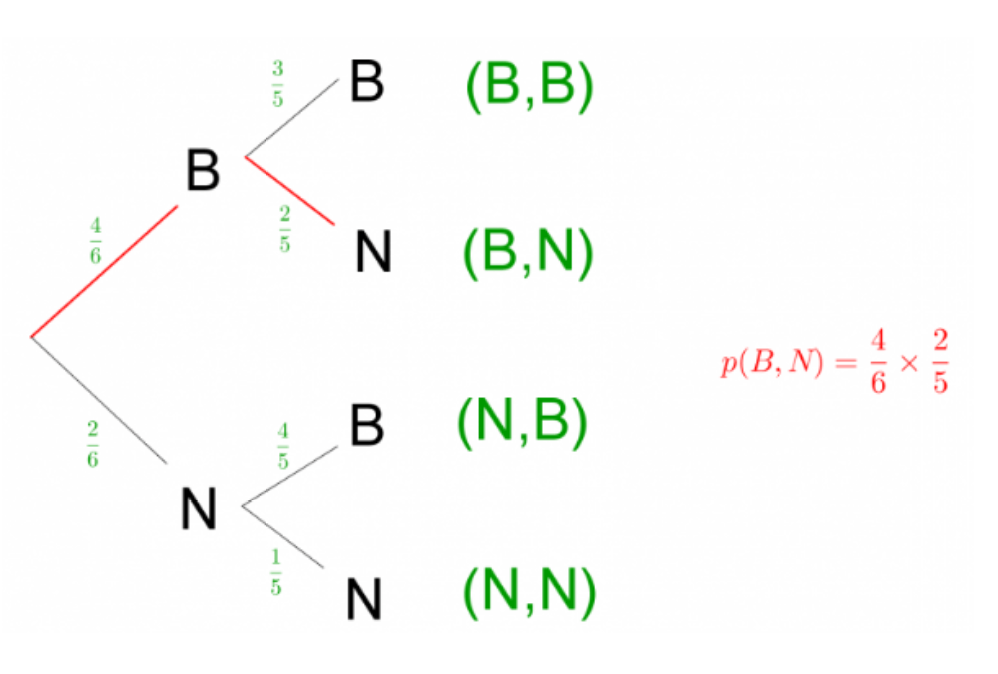
On en déduit alors l’arbre suivant :
On peut alors à l’aide de l’arbre déterminer la probabilité du résultat 
qui correspond au résultat de tirer une boule blanche suivi d’une boule noire : 
.
