Pour déterminer la loi de probabilité d’une variable aléatoire 
:
Etape 1 : On détermine l’ensemble 
des valeurs prises par la variable aléatoire .
Etape 2 : On détermine les probabilités des événements 
c’est-à-dire la probabilité pour que la variable aléatoire prenne la valeur 
.
Astuces :
- Il est recommandé de présenter si possible la loi d’une variable aléatoire sous forme de tableau comme celui qui suit :
|
 |
 |
 |
 |
 |
- Pour les élèves qui utilisent les chiffres avec virgules en faisant des arrondis, faire très attention car à la fin on doit toujours vérifier que la somme des probabilités des événements
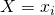est égale à 
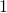c’est-à-dire que 
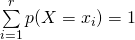, sinon revérifier vos calculs.
Exemple :
Considérons l’expérience qui consiste à tirer une boule d’une urne qui contient 
boules identiques au touchée numérotés de à (Parmi lesquelles les 
premières sont de couleur noir, les trois suivantes de couleur rouges et le reste de couleur blanches) et de noter la couleur et le numéro de la boule.
On définit un variable aléatoire comme suit :
Si la boule tirée ne porte pas un numéro pair, alors on perd 10€
Si la boule tirée porte un numéro pair et est de couleur blanche, on gagne 0€ (on ne gagne ni ne perd rien)
Si la boule tirée porte un numéro pair et est de couleur rouge, on gagne 5€ ;
Si la boule tirée porte un numéro pair et est de couleur noir, on gagne 10€.
Déterminer la loi de probabilité de .
L’ensemble 
.
C’est l’univers.
est l’ensemble des valeurs que peut prendre la variable aléatoire .
Les boules étant identiques, toutes les boules ont la même probabilité d’être tirées, il y a équiprobabilité.
L’événement 
correspond à l’événement :
« choisir une boule de numéro impair » = {1;3;5;7;9} = 
Ainsi 
L’événement 
correspond à l’événement :
« choisir une boule de numéro pair de couleur blanche » = {8;10} = 
Ainsi 
.
L’événement 
correspond à l’événement :
« Choisir une boule de numéro pair de couleur rouge » = {6} = 
Ainsi 
.
L’événement 
correspond à l’événement :
« Choisir une boule de numéro pair de couleur noir » = {2;4} = 
Ainsi 
.
On obtient donc la loi de :
|
-10€ | 0€ | 5€ | 10€ | Total |
|
 |
 |
 |
|
1 |
