Pour vérifier qu’une fonction ![]() est dérivable en un point
est dérivable en un point ![]() , et auquel cas déterminer le nombre dérivé de la fonction
, et auquel cas déterminer le nombre dérivé de la fonction ![]() au point
au point ![]() , on peut :
, on peut :
Etape 1 : Calculer la limite lorsque ![]() tend vers
tend vers ![]() du taux d’accroissement de la fonction
du taux d’accroissement de la fonction ![]() entre les points
entre les points ![]() et
et ![]() .
.
Cela revient à calculer : ![]()
Etape 2 : Conclusion :
Si cette limite existe et est finie, alors le nombre que l’on a trouvé est le nombre dérivé de la fonction ![]() en
en ![]() et se note
et se note ![]() . Et la fonction est dérivable en
. Et la fonction est dérivable en ![]() .
.
Sinon, la limite n’existe pas ou est infinie et la fonction n’est pas dérivable en ![]() .
.
Exemple :
Considérons les fonctions ![]() ,
, ![]() et
et ![]() définies comme suit :
définies comme suit :
![]() ,
, ![]() et
et ![]()
Etudier la dérivabilité de ![]() en
en ![]() , de
, de ![]() et
et ![]() en
en ![]() .
.
En déduire les éventuels nombres dérivés.
Cas de f :
Calculons le taux d’accroissement de ![]() entre
entre ![]() et
et ![]() :
:
![]() =
= ![]() =
= ![]() =
= ![]()
Conclusion :
Lorsque ![]() se rapproche de
se rapproche de ![]() ,
, ![]() se rapproche de
se rapproche de ![]() ,
,
Donc, ![]()
Ainsi ![]() est dérivable en
est dérivable en ![]() et son nombre dérivé en
et son nombre dérivé en ![]() est
est ![]() .
.
Cas de g :
Calculons le taux d’accroissement de ![]() entre
entre ![]() et
et ![]() :
:
![]() =
= ![]() =
= 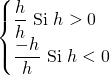 =
= 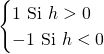
Lorsque, ![]() tend vers
tend vers ![]() avec des valeurs négatives, le taux d’accroissement est égale à
avec des valeurs négatives, le taux d’accroissement est égale à ![]() , et lorsque
, et lorsque ![]() tend vers
tend vers ![]() avec des valeurs positives, le taux d’accroissement est égale à
avec des valeurs positives, le taux d’accroissement est égale à ![]() .
.
Ainsi la limite lorsque ![]() tend vers
tend vers ![]() n’existe pas !
n’existe pas !
Conclusion :
![]() n’est pas dérivable en
n’est pas dérivable en ![]() . Le nombre dérivé de
. Le nombre dérivé de ![]() en
en ![]() n’existe pas.
n’existe pas.
Cas de k :
Calculons le taux d’accroissement de ![]() entre
entre ![]() et
et ![]() et calculons sa limite quand
et calculons sa limite quand ![]() tend vers
tend vers ![]() .
.
![]() .
.
![]() .
.
Conclusion :
![]() n’est pas dérivable en
n’est pas dérivable en ![]() . Donc n’admet pas de nombre dérivé en
. Donc n’admet pas de nombre dérivé en ![]() .
.
Astuce :
Pour la méthode 2,
A l’étape 1 : on calcule plutôt ![]() . Puis, on conclut de la même manière qu’à l’étape 2.
. Puis, on conclut de la même manière qu’à l’étape 2.
Exemple :
Etudier la dérivabilité en ![]() de la fonction
de la fonction ![]() définie par
définie par ![]()
Solution :
![]()
![]()
Donc ![]() est dérivable en
est dérivable en ![]() et son nombre dérivé est
et son nombre dérivé est ![]() .
.