1/ Prouver que la fonction 
n’est pas dérivable au point 
.
2/ Déterminer le nombre dérivé de 
au point 
.
3/ Déterminer l’ensemble de dérivabilité et la fonction dérivée des fonctions suivantes : ; et 
1/ Le domaine de définition de la fonction 
est 
.
Prouvons que la fonction n’est pas derivable en :
Le taux d’accroissement de la fonction entre et 
(
car doit appartenir à ) est donné par :
= 
= 
= 
= 
= 
.
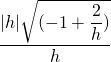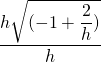Quand 
tend vers en restant positif, 
tend vers 
d’où $
