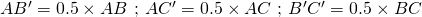Définition :
Une homothétie de rapport ![]() (avec
(avec ![]() entier relatif non nul) êrmet d’agrandir ou de réduire une figure à partir d’un point choisi comme centre, dans le rapport
entier relatif non nul) êrmet d’agrandir ou de réduire une figure à partir d’un point choisi comme centre, dans le rapport ![]() si
si ![]() ou dans le rapport
ou dans le rapport ![]() si
si ![]()
Exemple :
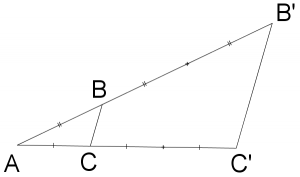
![]() est l’image du triangle
est l’image du triangle ![]() par l’homothétie de centre
par l’homothétie de centre ![]() et de rapport
et de rapport ![]() .
.
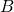 et
et 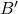 (respectivement
(respectivement 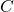 et
et 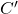 ) sont alignés avec
) sont alignés avec 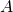 et du même côté par rapport à
et du même côté par rapport à 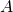
- Les droites
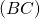 et
et 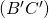 sont parallèles
sont parallèles 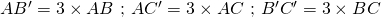
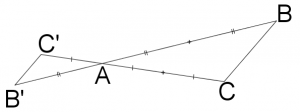
![]() est l’image du triangle
est l’image du triangle ![]() par l’homothétie de centre
par l’homothétie de centre ![]() et de rapport
et de rapport ![]() .
.
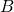 et
et 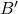 (respectivement
(respectivement 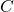 et
et 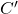 ) sont alignés avec
) sont alignés avec 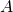 et de part et d’autre de
et de part et d’autre de 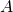
- Les droites
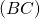 et
et 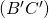 sont parallèles
sont parallèles