1.1 Uniquement à l’aide des normes
Dans toute la suite, l’espace est muni d’un repère orthonormé direct ![]() .
.
Soient ![]() et
et ![]() deux vecteurs de l’espace.
deux vecteurs de l’espace.
Le produit scalaire de ![]() et
et ![]() note
note ![]() est le reel
est le reel ![]()
Exemple:
Soient ![]() et
et ![]() trois points de l’espace tels que
trois points de l’espace tels que ![]() et
et ![]() .
.
Calculer ![]() et
et ![]() .
.
Solution
(1) 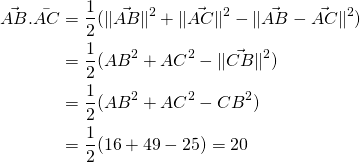
(2) 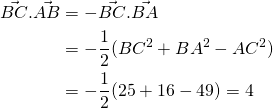
1.2 Normes et angle des deux vecteurs
Soient ![]() et
et ![]() deux vecteurs de l’espace.
deux vecteurs de l’espace.
Le produit scalaire de ![]() et
et ![]() est
est ![]() .
.
Conséquences immediates
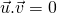 si et seulement si les vecteurs
si et seulement si les vecteurs 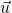 et
et 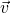 sont orthogonaux (
sont orthogonaux (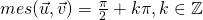 ).
).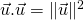 . On note
. On note 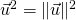 (
(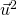 est appele carre scalaire).
est appele carre scalaire).- Si
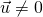 et
et 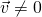 alors
alors 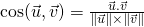 .
. - Si
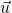 et
et 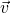 sont colinéaires de même sens alors
sont colinéaires de même sens alors 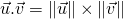 .
. - Si $\vec{u}