est un carré de côté 
. 
désigne le milieu du segment 
et 
est le milieu du segment 
.
et 
sont des points respectivement situés sur les segments et 
tels que 
.
On pose 
.
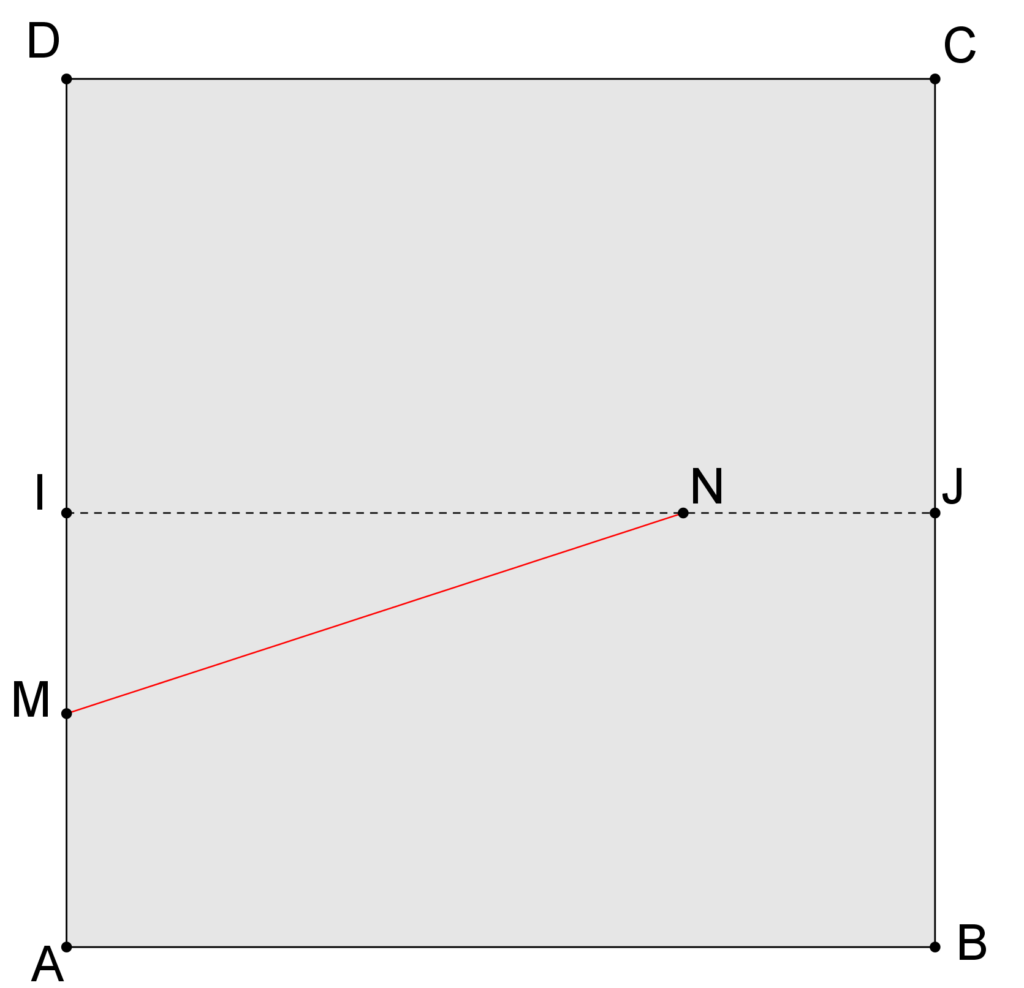
1. Démontrer que 
(il y a deux cas à considérer).
2. Montrer que 
3. Soit 
la fonction définie sur 
. par 
a) Etudier les variations de g et dresser son tableau de variation.
b) Le plan est rapporté à un repère orthogonal 
(unités pour le repère : 
en abscisse ;
en ordonnée). Montrer que la droite d’équation 
est un axe de symétrie de la courbe représentative de .
c) Tracer cette courbe.
4. Représenter la fonction 
sur le graphique précédent ; pour quel réel 
, la distance 
est-elle minimale ?
1. Si , 
alors 
On a alors 
