Méthode 5 : Comment déterminer 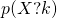 ou
ou 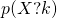 lorsque
lorsque 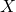 suit la loi binomiale ?
suit la loi binomiale ?
Pour déterminer les probabilités des événements de la forme :
« Obtenir au plus ![]() succès à la fin de fin de l’expérience » c’est calculer
succès à la fin de fin de l’expérience » c’est calculer ![]()
Ou « obtenir au moins ![]() succès à la fin de fin de l’expérience » c’est calculer
succès à la fin de fin de l’expérience » c’est calculer ![]() , lorsque
, lorsque ![]() suit la loi binomiale
suit la loi binomiale ![]() , il suffit d’appliquer les formules suivantes :
, il suffit d’appliquer les formules suivantes :
![]()
![]()
![]()
Exemple :
Expérience : On lance dis fois un dé à 6 faces, dont les faces sont numéroté de 1 à 6. Lors d’un lancé, si le numéro qui apparait est 1 alors c’est un succès, sinon c’est un échec.
On note ![]() la variable aléatoire qui compte le nombre de succès de cette série de
la variable aléatoire qui compte le nombre de succès de cette série de ![]() lancers.
lancers.
Déterminer la probabilité d’avoir au plus ![]() succès et celle d’avoir au moins
succès et celle d’avoir au moins ![]() .
.
Déterminer la probabilité d’avoir au plus ![]() succès
succès
Solution :
L’événement « avoir au plus 4 succès » correspond à « ![]() » Ainsi la probabilité qu’on cherche c’est :
» Ainsi la probabilité qu’on cherche c’est :

Et il suit que la probabilité de l’événement contraire : « avoir au moins 5 succès » est :
![]()
Ici on cherche ![]() .
.
Mais déterminer cette probabilité en utilisant directement la formule ![]() n’est pas éfficase du tout ! au contraire c’est plustôt très fastidieux car la somme englobe 8 termes à calculer.
n’est pas éfficase du tout ! au contraire c’est plustôt très fastidieux car la somme englobe 8 termes à calculer.
Il est donc préférable de déterminer la probabilité de l’événement contraire c’est-à-dire ![]() qui contient seulement 3 termes à calculer.
qui contient seulement 3 termes à calculer.
Ainsi on a :
![]() =
= ![]() =
= ![]() =
= ![]()
Il vient alors que ![]()
Résultat intéressant !! il est presque impossible d’avoir plus de 8 succès …