On considère une variable 
qui suit une loi binomiale de paramètre 
, 
.
Pour déterminer l’intervalle de fluctuation de avec une certitude de plus de 
que se trouvera bien dans cette intervalle de fluctuation, on procède comme suit :
Etape 1 : On détermine à l’aide d’un tableur les probabilités 
, 
variant entre 
et en procédant comme suit :
Dans les cellules suivantes :
A1, on écrit .
B1, on écrit 
puis on sélectionne les cases A1 et B1 et on tire de la gauche vert la droite à partir du petit rectangle noir en bas à droite des deux cases sélectionnées et on s’arrête lorsqu’on a tous les nombres de à .
A2, on écrit =LOI.BINOMIALE(A1 ; n ; p ; VRAI) puis on choisi la case A2 et on tire de la gauche vert la droite à partir du petit rectangle noir en bas à droite de la case A2 et on s’arrête lorsqu’on à la dernière case du tableau.
Etape 2 : On note 
le premier entier tel que 
et 
.
Etape 3 : On note 
le premier entier tel que 
et 
.
Etape 4 : On conclut que 
est l’intervalle de fluctuation pour les valeurs de avec une probabilité supérieure à 
, et 
est l’intervalle de fluctuation de la proportion (la fréquence 
).
Exemple intervalle de fluctuation :
Une enquête est ouverte sur une entreprise automobiliste. Le gouvernement souhaiterait avoir une idée de la proportion des véhicules jugés défectueux après fabrication.
L’entreprise maintient que la proportion de véhicule défectueux est 0,04. L’enquête est menée sur 400 véhicules. Soit la variable aléatoire qui compte le nombre de véhicule défectueux.
Déterminer l’intervalle de fluctuation de et l’intervalle de fluctuation de la proportion.
On peut considérer que suit une loi binomiale de paramètre 400 et 0,04. Car l’enquête peut être vu une suite de 400 expériences indépendantes et identiques (vu que la population est de grande taille), chacune des expériences ayant deux issues : véhicule défectueux (succès) avec une probabilité de 0,04 ou véhicule en bonne état (échec) avec une probabilité de 0,96.
Ensuite, utiliser le tableur dans lequel on a les valeurs des , 
Puis, lire ensuite la valeur de 
ainsi que la valeur de 
comme présenté dans les figures 1 et 2 qui suivent :
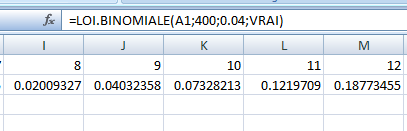
Figure 1
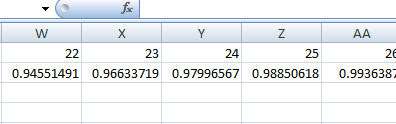
Figure 2
Il suit que [9;24] et [0,0225;0,06] sont respectivement l’intervalle de fluctuation de et l’intervalle de fluctuation de la proportion.
