A. Règles fondamentales
On ne change pas une égalité quand :
- On additionne ou on retranche un même nombre aux deux membres d’une égalité
- On multiplie ou on divise par un même nombre non nul les deux membres d’une égalité.
B. Méthodes de résolution
Cas 1 : Équations de base du type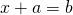 
ou 
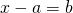
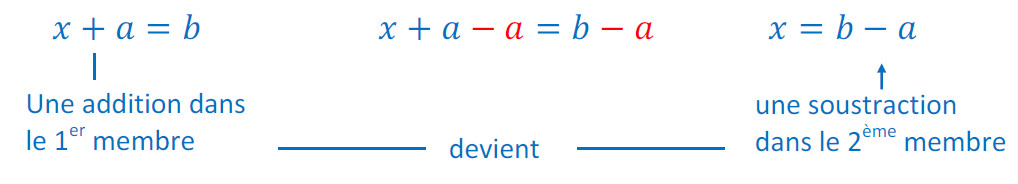
Exemple :
On peut vérifier la solution : 
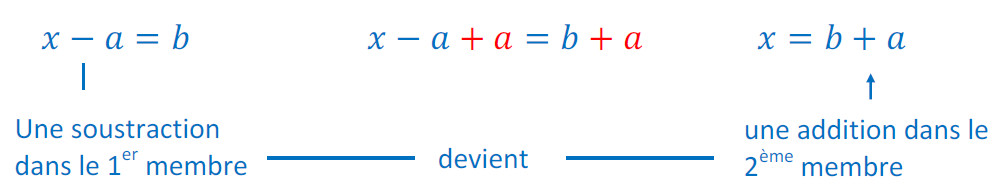
Exemple :
On peut vérifier la solution : 
Cas 2 : Équations de base : du type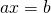 
ou 
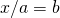
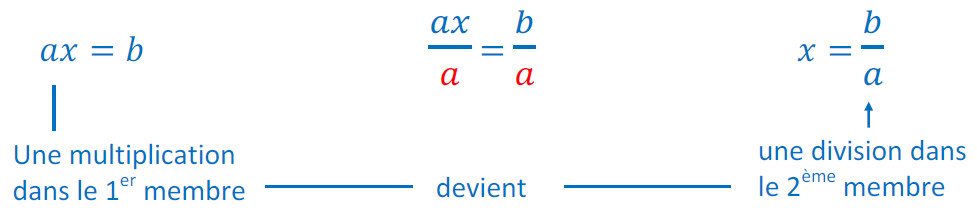
Exemple :
On peut vérifier la solution : 
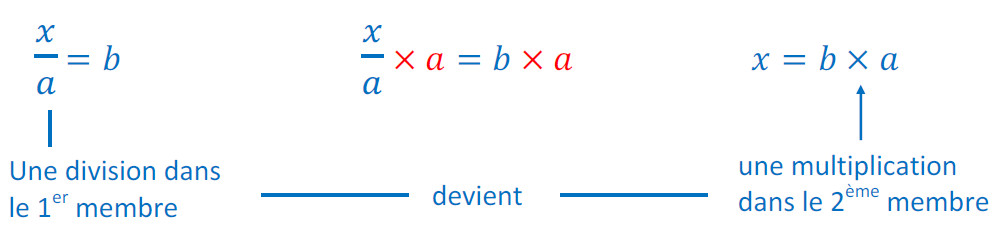
Exemple :
On peut vérifier la solution : 
Cas 3 : Equations du type :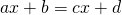 
Méthode :
On regroupe :
- dans le premier membre, tous les termes en
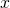
- dans le second membre, tous les nombres
Exemple 1 :
On regroupe les termes en x et les nombres
Exemple 2 :
Dans ce cas, la division ne s’arrête pas.
On laisse le résultat 
Cas 4 : Méthode générale
On développe et on réduit dans chaque membre pour se ramener à une équation du type , puis on résout cette équation.
Exemple :
Dans le membre de gauche, on applique la distributivité
Et pour le membre de roite, on fait une suppression des parenthèses derrière un signe –
C. Equation-produit
Exemple :
Cette égalité est vérifiée pour et pour .
Propriété
Un produit de facteurs est nul si un au moins des deux facteurs est nul et réciproquement.
Exemple de rédaction
Résoudre l’équation suivante :
Cette équation est une équation-produit.
Or, un produit de facteurs est nul si un au moins des deux facteurs est nul et réciproquement.
Donc, 
ou 
ou 
L’équation a deux solutions : et
D. Mise en équation d’un problème
Certains problèmes peuvent se résoudre en posant une équation.
Méthode :
On procède en 4 étapes :
Etape 1 : On choisit l’inconnue
Etape 2 : On écrit l’équation (on transcrit la phrase en français par une équation)
Etape 3 : On résout l’équation.
Etape 4 : On rédige la réponse.
Exemple :
A la boulangerie, Pierre achète un pain et trois baguettes. Le tout coûte 4 euros. Le pain coûte deux fois plus cher qu’une baguette.
Combien coûte une baguette ? Combien coûte un pain ?
Solution :
Etape 1 : Choix de l’inconnue
soit x le prix d’une baguette
Etape 2 : Mise en équation
4 euros représente le prix des 3 baguettes (3x) et du pain (2x)
Etape 3 : Résolution de l’équation
Etape 4 : Rédaction de la solution
Une baguette coûte 0,8 euros. Un pain coûte 1,6 euros.
