1.1 Théorème de Moivre Laplace
Definitions
On dit qu’une variable aléatoire est centrée et reduite lorsque son esperence est nulle et son écart type est égal à 1.
Remarque :
Si 
est une variable aléatoire prenant un nombre fini de valeurs d’esperence 
, de variance 
et d’écart type 
; alors la variable aléatoire 
est une variable aléatoire centrée reduite.
En effet :
= 
= 
= 
= 
= 
.
= 
= 
= 
=
= 
.
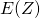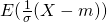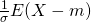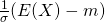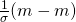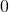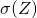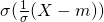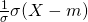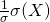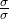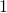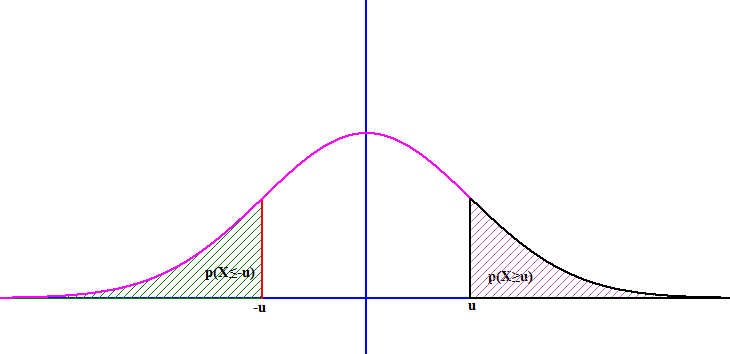
Théorème (Moivre Laplace)
Soit 
un nombre de l’intervalle 
. Soit 
une suite de variable aléatoire de loi binomiale 
. On pose 
qui est une variable aléatoire centrée reduite associée a 
(
et 
). Alors pour tous réels 
et 
tels que 
on a 
.
1.2. Loi reduite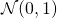 
Propriété :
La fonction 
est une densité de probabilité sur 
.
Definition :
Une variable aléatoire suit la loi centrée reduite si sa fonction densité est la fonction 
definie sur par 
.
On a alors pour tous réels et tels que 
Propriété :
Soit une variable aléatoire qui suit la loi normale , on a:
- Pour tout réel positif
; 
.
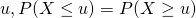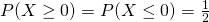