I. Fonction dérivée ; équation d’une tangente

1.1 Fonction dérivable en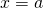

Soit une fonction dérivable sur un intervalle . soit un r\’eel appartenant\`a . On dit que d\’erivable en signifie que la limite quand tend vers du quotient  existe et est un nombre réel.

On note alors ou encore

s’appelle le nombre dérivé de en .

1.2 Fonction dérivée

• Si 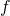est dérivable en tout point 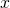de 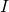, on dit que 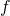est dérivable sur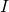
  on d\’efinit ainsi la fonction dérivée par 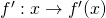pour tout point 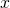de .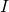
• Le calcul de la d\’eriv\’ee d’une fonction repose d’une part sur la connaissance des dérivées des fonctions usuelles , et d’autre part sur les règles de dérivation appliquées aux opérations sur les fonctions d\’erivables.

1.3 Equation de la tangente en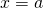

Soit une fonction d\’erivable sur I, la courbe repr\’esentative de f dans un repère.

• La tangente à 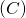 au point A de coordonnée 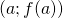est la droite passant par A et de coefficient directeur 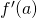. Elle a donc pour equation .
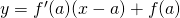• Pour connaitre la position relative de par rapport à sa tangente, on étudie le signe de 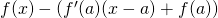.