Dans un récipient de forme cylindrique de rayon 4 
, on place une première boule 
de rayon 2. On verse en suite de l’eau jusqu’à recouvrir exactement cette boule; On dit que la surface de l’eau est tangente à la boule. On retire la boule sans modifier le volume d’eau. On la remplace par une autre boule 
, de rayon inconnu 
, différent de celui de . On s’appercoit que le niveau de l’eau est encore tangent à la boule. Le but de ce problème est de trouver le rayon 
.
a. Calculer le volume d’eau versé 
lorsqu’il y avait la boule , exprimée en 
.
b. Calculer le volume << boule + eau >> de deux facons différentes.
c. En déduire que doit être solution de l’équation :
(1) 
d. On connait déja une solution de cette équation. Laquelle ? et pourquoi ? Vérifier ce résultat par calcul.
e. Montrer que 
.
f. écrire 
sous la forme 
, où 
et 
sont des réels à déterminer.
g. Finir la résolution et conclure.
a.
Le volume d’eau versé est celui d’un cylindre de hauteur 
et de rayon , duquel on soustrait le volume d’une boule de rayon 
.
On obtient : 
b. Globalement, ce volume est celui d’un cylindre de hauteur 
, c’est – à – dire : 
.
En séparant les volumes de la boule et de l’eau, ce volume s’écrit : 
.
c. On obtient l’équation :
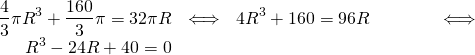
d. 2 est solution de cette équation; Ce nombre correspond au rayon de la boule. On obtient 
e. 
.
f. D’après une identité remarqua
