Exercice :
Soit 
la fonction définie sur 
par 
et 
sa courbe représentative.
1/
a) Calculer 
.
b) On prolonge la définition de à 
en posant 
. Comment choisir 
pour que soit continue sur ?
2/
a) Calculer les limites de 
en 
et 
.
b) Déterminer une condition suffisante sur 
pour que 
.
c) Interpréter graphiquement les résultats précédents.
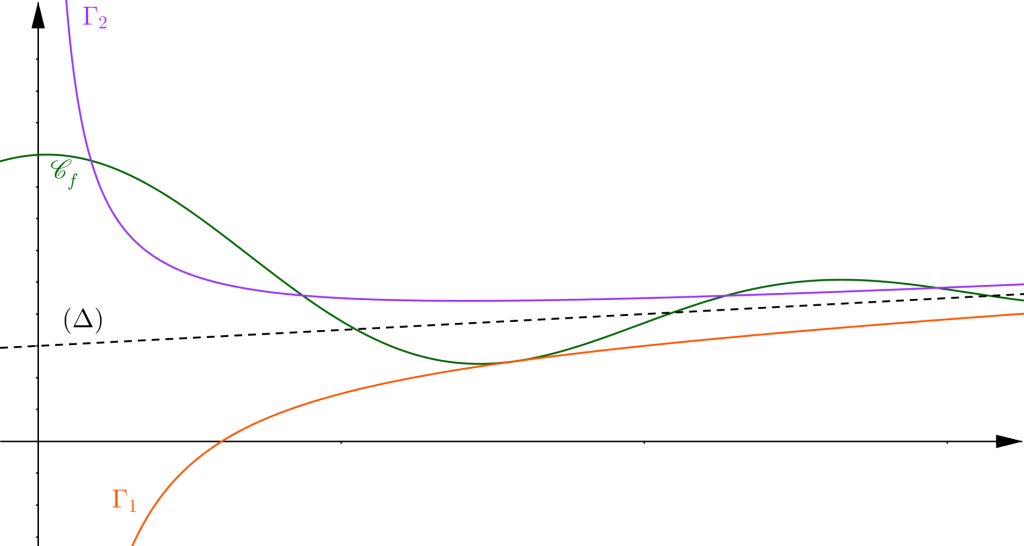
3/ On dispose, ci-contre, du tracé sur 
de , de celui de la droite d’équation 
, ainsi que des courbes 
et 
représentant respectivement les fonctions 
et 
définies sur par :
et 
.
Déterminer l’abscisse de chacun des points 
, 
et 
.
Solution :
La solution de cet exercice sera bientôt disponible.
Pour recevoir cette solution par email, contactez-
