On considère l’énoncé suivant: Grâce à son entraînement et à son expérience, un sportif adepte du sémi-marathon sait que : S’il a terminé la course lors de son précédent sémi-marathon, il terminera le prochain sémi-marathon avec une probabilité de 
;
S’il a abandonné lors de son précédent sémi-marathon, il terminera le prochain sémi-marathon avec une probabilité de 
.
Ce sportif a terminé son sémi-marathon de janvier 
. Pour tout entier naturel 
on note 
la matrice ligne 
traduisant l’état probabiliste du -ième mois écoulé depuis janvier où 
désigne la probabilité que ce sportif abandonne au sémi-marathon du – mois et 
celle qu’il termine le sémi-marathon du -ième mois.
L’état probabiliste initial correspondant à janvier est donc 
- Donner un graphe probabiliste à sommets
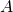et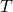 
traduisant la situation. - Donner la matrice de transition de ce graphe.
- Quelle est la probabilité que ce sportif termine le sémi-marathon de fevrier ?
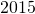