4. Ecriture trigonométrique d’un nombre complexe

A. Introduction au module d’un nombre complexe

Soit d’affixe  dans le répère 

 

 

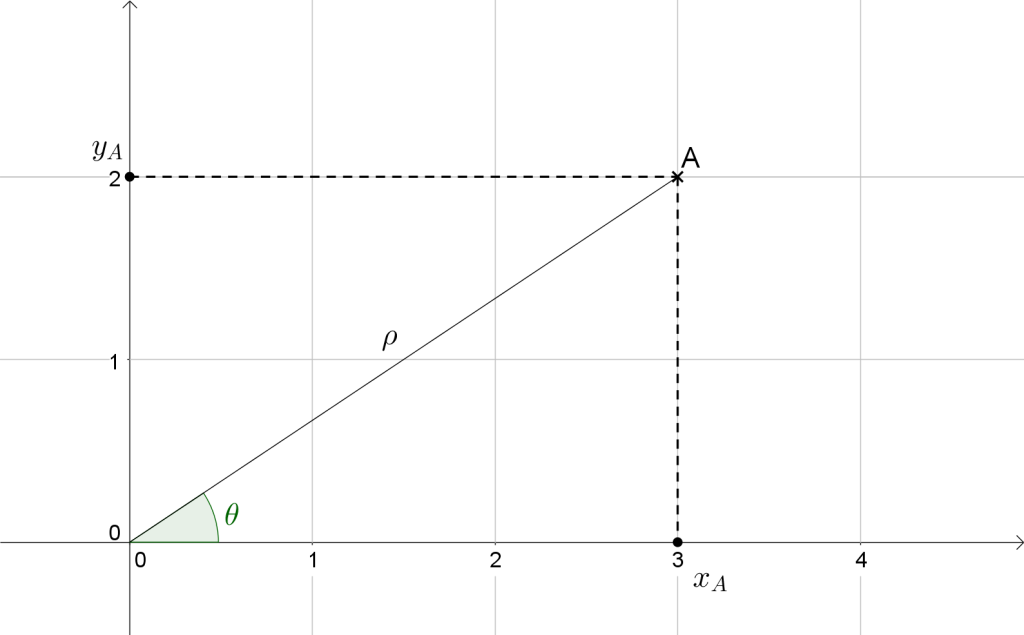
et 

 

On a donc :

avec 

avec 

Avec pythagore, , donc  et ainsi 

On déduit que :

et

et donc, 

 

 

B. Définition et propriétés

Définition :

Le plan est muni d’un repère orthonormal 

Soit  un nombre complexe non nul, affixe d’un point .

L’écriture trigonométrique de  est  avec 

Avec  et 

sont les coordonnées polaires de M 

se nomme « le module de z » et se note 

se nomme « argument de z » et se note 

 

Exemple :

Donner la forme trigonométrique du complexe 

 

 

Propriétés :

Pour tout nombre complexe  non nul,, on a :

 

 

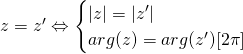
Propriétés :

Pour tous nombres complexes et , on a :

pour tout entier naturel n

Pour  

Pour  

 

 

C. Module, argument et géométrie

Propriété :

Le plan est muni d’un repère orthonormal 

Soient  et des nombres complexes non nuls, affixes des points et . On a alors :

 

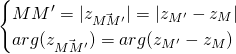
Exemple :

On a les nombres complexes et  dans le repère 

Calculer  et , puis