A – Suites arithmétiques
Définition :
Pour une suite 
, il est équivalent de dire :
- Le terme général est
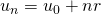
- Elle vérifie la relation de récurrence : Pour tout entier naturel n,
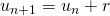
On dit que la suite est une suite arithmétique de raison 
La somme des 
premiers termes est : 
Exemples :
La suite des entiers naturels est une suite arithmétique de raison 
.
Et pour tout entier , 
.
Cette formule est à retenir car peut vous être très utile.
B – Suites géométriques
Définition :
Dire qu’une suite est géométrique signifie qu’il existe un réel 
non nul tel que pour tout entier naturel : 
.
Expression de 
en fonction de : 
La somme de ses premiers termes est :
Si 
, 
Exemples :
La suite 
est une suite géométrique de raison 
La suite 
est une suite géométrique de raison 
Convergence de suite géométrique :
Les résultats suivants sont admis :
- Si
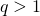, Alors la suite 
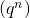est croissante
- Si
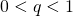, Alors la suite 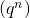est décroissante
- Si 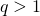, Alors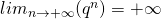
- Si
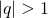, Alors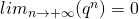 
Le saviez-vous ?
La suite 
est croissante et de limite 
La suite 
n’est pas monotone mais elle a pour limite 
La suite 
est décroissante et a pour limite
