Comment utiliser le cercle trigonométrique : Guide complet
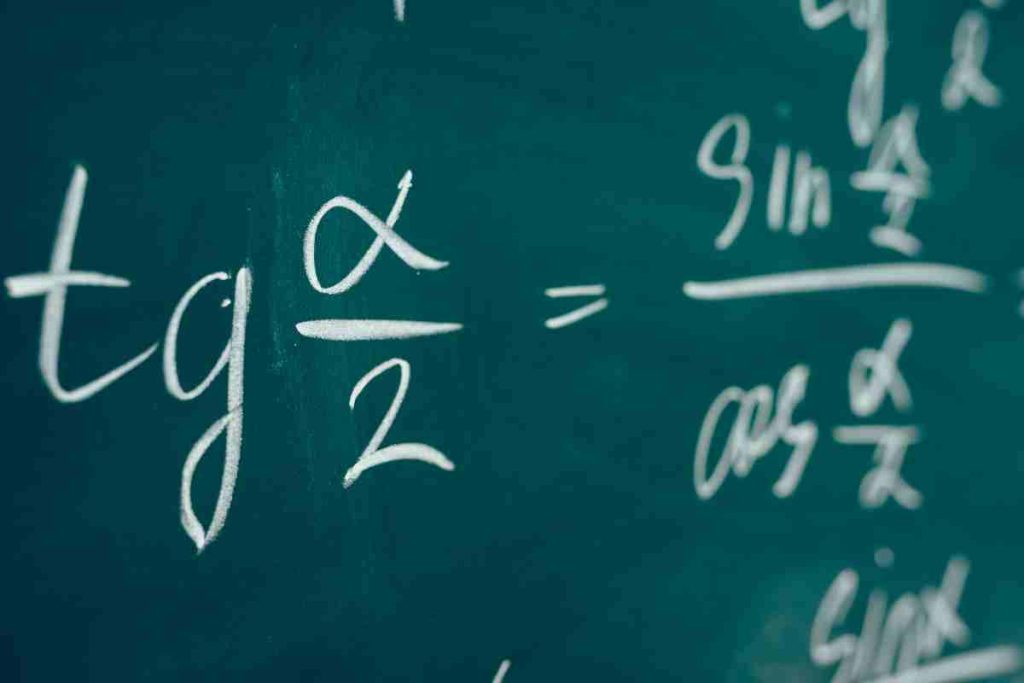
1. Les bases du cercle trigonométrique
Le cercle trigonométrique est un outil fondamental en mathématiques qui permet de visualiser et comprendre les relations trigonométriques. C'est un cercle de rayon 1 centré à l'origine du repère orthonormé.
1.1 Lecture des coordonnées
Sur le cercle trigonométrique, pour un angle α donné :
- Le cosinus correspond à l'abscisse du point M (projection sur l'axe x)
- Le sinus correspond à l'ordonnée du point M (projection sur l'axe y)
- La tangente est le rapport entre le sinus et le cosinus : tan(α) = sin(α)/cos(α)
2. Relations fondamentales pour les angles remarquables
2.1 Angle opposé (-α)
Pour tout angle α, son opposé -α vérifie :
- cos(-α) = cos(α)
- sin(-α) = -sin(α)
- tan(-α) = -tan(α)
2.2 Angle complémentaire (π - α)
Pour l'angle π - α :
- cos(π - α) = -cos(α)
- sin(π - α) = sin(α)
- tan(π - α) = -tan(α)
2.3 Angle supplémentaire (π + α)
Pour l'angle π + α :
- cos(π + α) = -cos(α)
- sin(π + α) = -sin(α)
- tan(π + α) = tan(α)
3. Exemples pratiques
Prenons un exemple concret : Si pour un angle α on a :
- cos(α) = 0.5
- sin(α) = 0.866
Alors :
| Angle | Sinus | Cosinus | Tangente |
|---|---|---|---|
| α | 0.866 | 0.5 | 1.732 |
| -α | -0.866 | 0.5 | -1.732 |
| π - α | 0.866 | -0.5 | -1.732 |
| π + α | -0.866 | -0.5 | 1.732 |
4. Points clés à retenir
- Le cercle trigonométrique est un cercle unitaire (rayon = 1)
- Les coordonnées d'un point M sur le cercle donnent directement les valeurs de sin et cos
- La tangente peut être calculée comme le rapport sin/cos
- Les relations entre angles sont basées sur des symétries dans le cercle
Go up
Laisser un commentaire